| Home » Articles » LESSON NOTES (Mathematics) » High School level |
|
DISTANCE BETWEEN TWO POINTS
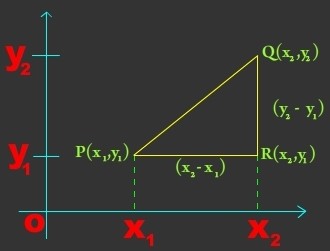
Consider the figure below:
Let P and Q be points with coordinates (x1,y1) and (x2,y2) respectively as shown above. PQR is right angled triangle. By Pythagoras theorem: PQ2 = PR2 + RQ2 = (x2-x1)2 + (y2 – y1)2
Therefore: PQ2 = (x2-x1)2 + (y2 – y1)2
Example #1 Find the distance between points (5,-2) and (2,2) Solution: From the above points: x1 = 5, y1 = -2 and x2 = 2, y2 = 2 Therefore by distance formula: PQ2 = (x2-x1)2 + (y2 – y1)2 Distance =√[ (5 – 2)2 + (-2 -2)2] Distance =√[ 32 + (-4)2] = √ (9 + 16) = √[ 25] Therefore, the distance = 5 units
Example #2 Prove that the Triangle with vertices given by A(3,5), B(-1,-1) and C(4,4) is a right angled triangle. Solution: AB2 = (-1 - 3)2 + (-1 - 5)2 AB2 = 16 + 36 = 52
BC2 = (-1 - 4)2 + (-1 - 4)2 BC2 = 25 + 25 = 50
AC2 = (4 - 3)2 + (4 - 5)2 AC2 = 1 + 1 = 2
Relating the three sides we found that: AB2 = BC2 + AC2 Hence Triangle ABC is the right angled triangle.
Try yourself:
1 .Find the distance between each of the following points: (a) A(6,2) and B(-2,4) (b) C(-2,2) and D(8,-2) (c) E(3,1) and F(-2,6) (d) G(3,7) and H(9,-2) 2. Find the perimeter of triangle given by vertices (2,1) , (6,1) and (6,4) 3. Find the area of the Triangle with vertices given by A(3,5), B(-1,-1) and C(4,4) 4. Given points: A(3,1), B(0,6) and C(-5,3). Prove that triangle PQR is isosceles.
********Thanks for reading and have a nice day****** Added By (Yahyou M) - BADSHAH
| |
| Views: 782 | | |
| Total comments: 0 | |