| Home » Articles » LESSON NOTES (Mathematics) » High School level |
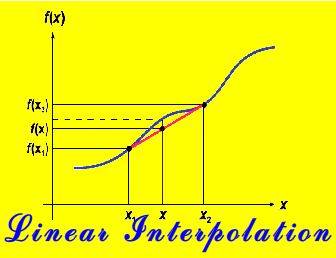
LINEAR INTERPOLATION
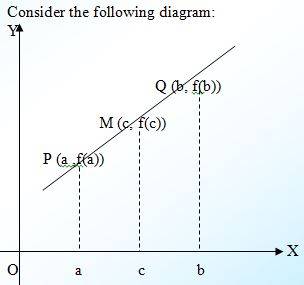
Consider the following diagram:
Let M be the slope of the straight line PQ then M = [f(b) – f(a)]/ (b – a) ------------------- (I) Also M = [f(c) – f(a)]/ (c – a) Since both are the value of the slope M then [[f(b) – f(a)]/ (b – a)] = [[f(c) – f(a)]/ (c – a)] then by making subject f(c) the equation will become: this is called linear interpolation... Read more this article
Application of linear interpolation:
Example #1: The function f(x) takes the following values:
Using linear interpolation find the value of 2.2. Solution: From the table above 2.2 is found between 2 and 3, f (2) and f (3) then from the formula F (b) = 0.25, F (a) = 0.33, b = 3, a= 2 and c is the given number that is 2.2 so we need to find F (2.2), By substitution from the formula F (2.2) = 0.314. There fore the value of 2.2 is 0.314
Example #2 Given that e1.25 = 3.4903 and e1.26 = 3.5254 find e1.257 by using linear interpolation. Solution: From the question x = 1.25 and 1.26 then in the table will be
From the above 1.257 lies between 1.25 and 1.26 then using the formula F (b) = 3.5254, F (a) = 3.4903, a = 1.25, b= 1.26 and c is the given number that is 1.257 then we need to find F (1.257). By substitution in the linear interpolation the answer will be 3.5149 There fore e1.257 = 3.5149.
Example #3 If sin 35˚ = 0.5736 and sin 40˚ = 0.6428 find sin 37˚ by using linear interpolation. Solution:
37˚ lies between 35˚ and 40˚ then from the equation F (b) = 0.6428, F (a) = 0.5736, b = 40, a = 35 and c is the given angle that is 37˚ then we need to find F (37). After substitution to linear interpolation the value of sin 37˚ is 0.60128 Qn: Given that log (1.96) = 0.2923 and log (1.97) = 0.2945, using linear interpolation find the number for which log (x) = 0.2935.
--------------END OF LINEAR INTERPOLATION --------------------- | |||||||||||||||||||||
| Views: 861 | | | |||||||||||||||||||||
| Total comments: 0 | |