| Home » Articles » LESSON NOTES (Mathematics) » Upper Primary |
AREA OF THE SHADED PART NOTES CODE: MT160081ES
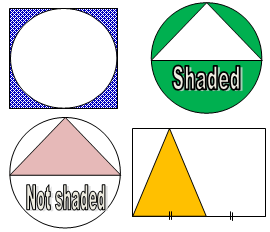
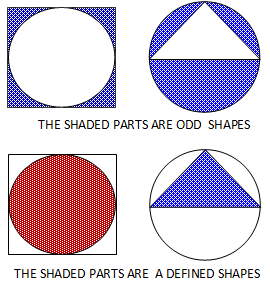
In this tutorial, we shall see how areas of shaded parts are obtained by using different techniques. Remember, before you learn this, you have to acquire the good knowledge of how to identify the polygons involved in a question of finding the area of shaded part and to have the knowledge of finding areas of different shapes. Sometimes, shaded part can be a defined polygon or cannot be a defined polygon (odd shape) as the pictures below:
PART A: FINDING THE AREA OF SHADED PART OF THE DEFINED SHAPE If the shaded part is a defined shape, identify the dimensions and find the area of the defined shape.
Examples #1: Find the area of the shaded part below:
Solution: The shaded part is a circle with radius 7m, so your task is only to find the area of that circle, ignore the triangle. Area = πr2 = 22/7 x 7m x 7m = 154m2 Therefore the area of the shaded part = 154 m2
Examples #2: Find the area of the shaded part below:
Solution: The shaded part is a square with diagonal 10m, so your task is only to find the area of that square, ignore the circle. Note that, the diagonal of the square is the same as the Diameter of the given circle as shown above, so you have to use different techniques to obtain the dimensions of the required polygon. The area of the square by using diagonal is given by: Area = (d x d)/2 or ½ of the square of diagonal Area = (10m x 10m) /2 = 100m2 /2 = 50m2 Therefore the area of the shaded part = 50 m2
Examples #3: Find the area of the shaded part below:
Solution: The shaded part is a semi-circle with diameter 14cm, so find the area of the semi-circle, and ignore the rectangle. You have to note that, the length of the rectangle is equal to the Diameter of the semi-circle:- Area = 1/2πr2 but we have Diameter, to get Radius simply divide Diameter by 2, so from our question the radius will be 7 cm. Therefore: Area = ½ x 22/7 x 7cm x 7cm = 77 cm2 Therefore the area of the shaded part = 77 cm2
PART B: FINDING THE AREA OF THE ODD SHAPED SHADED PART Sometimes the shaded part cannot be defined i.e. odd shape, you can’t define it whether it is a rectangle, square, trapezium or any defined shape by its name. These questions nearly always involve subtraction. Usually, all you have to do is subtract the white area from the area of the whole figure. So in this condition you need to follow the following steps: Find the area of the whole polygon then find the area of the white polygon then use: (The area of the whole shape) – (the area of the white shape) = the area of the shaded part
Examples #1: Find the area of the shaded part below:
Solution: The shaded part is the odd shape, so follow the steps below: (i) Find the area of the rectangle = 14cm x 20cm = 280cm2 (ii) Find the area of the semi-circle = 77 cm2 (we assume that you have prior knowledge of finding areas) if you face any difficulties concerning how to find the areas please click here to learn about it. (iii) Take 280cm2 - 77 cm2 = 203 cm2 Therefore the area of the shaded part = 203 cm2
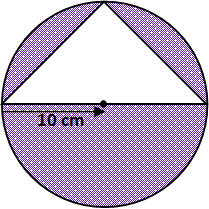
Examples #2: Find the area of the shaded part below:
Solution: The shaded part is the odd shape, so follow the steps below: The whole shape is a circle with radius 10 cm The white area inside is a triangle with the following dimensions (i) Base = Diameter of the circle = 20 cm (ii) Height = Radius of the circle = 10 cm Therefore find the areas of the polygons as follows: (i) The area of the circle = PI x r x r = 3.14 x 10cm x 10cm = 314cm2 (ii) The area of the triangle = ½ x Base x height = ½ x 20cm x 10cm = 100cm2 To get the shaded part take the area of the whole polygon, this is the circle minus the area of the triangle: Then, 314cm2 - 100cm2 = 214cm2 Therefore the area of the shaded part = 214 cm2
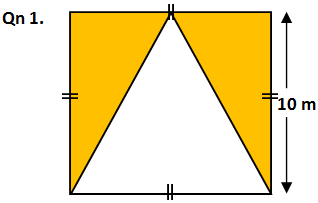
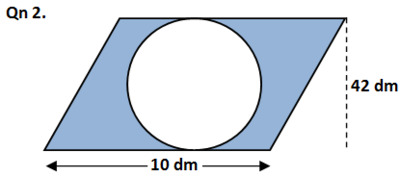
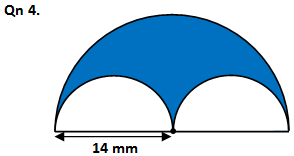
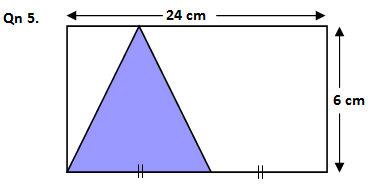
TRY YOURSELF AND COMMENT THE ANSWERS BELOW: Find the areas of the shaded parts below:
************** END ****************** In case of any question or comment be free to write down:
A lot of Thanks  Mr. Yahya M (Badshah) ****** MT160081ES *******
| |
| Views: 716 | | |
| Total comments: 0 | |